Variables e Inecuaciones Matemáticas

Variables en Matemáticas

primera parte

 df de variable una variable es un símbolo constituyente de un predicado, fórmula, algoritmo o de una proposición.

Variable independiente

• Una variable independiente es aquella cuyo valor no depende del de otra variable.
• La variable independiente en una función se suele representar por x.
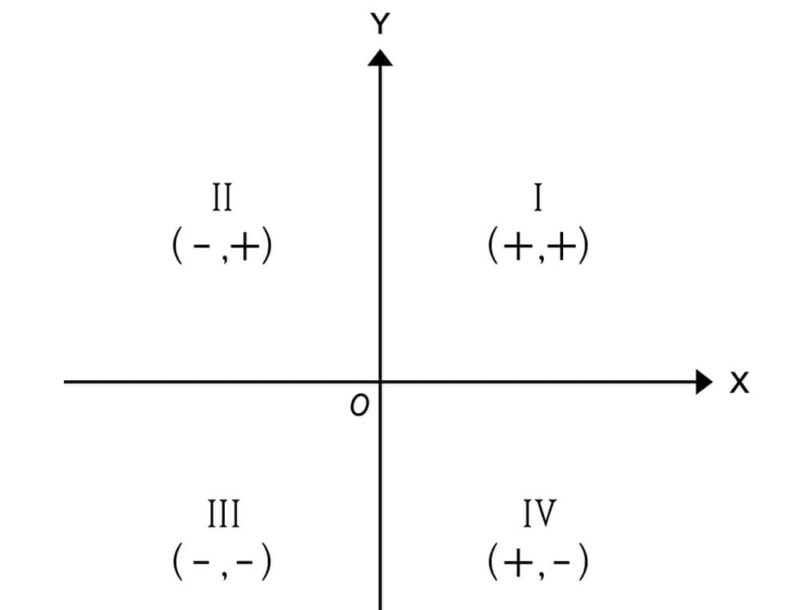
• La variable independiente se representa en el eje de abscisas.

Variable dependiente.

• Una variable dependiente es aquella cuyos valores dependen de los que tomen otra variable.
• La variable dependiente en una función se suele representar por y.
• La variable dependiente se representa en el eje ordenadas.
• La variable y está en función de la variable x.

EJERCICIO 1

Resuelve y grafica la desigualdad 5x-10

Paso 1: Aquí, no tenemos nada para simplificar, por lo que empezamos con: 5x-10

Paso 2: Para despejar la variable, sumamos 10 de ambos lados y simplificamos: 5x-10+10= 5x

Paso 3: Para resolver, dividimos ambos lados por 5: 5/5x= x

Paso 4: Para graficar, notamos que las soluciones a la desigualdad son todos los números reales hacia la izquierda de 5. El 5 no está incluido, por lo que usamos un punto vacío para indicar esto: 0

EJERCICIO 3

Resuelve la desigualdad 5x+3>3x-3.

Paso 1: No tenemos nada para simplificar. Empezamos con la desigualdad: 5x+3>3x-3

Paso 2: Restamos 3 y 3x de ambos lados para despejar la variable: 5x+3-3-3x>3x-3-3-3x = 2x>-6

Paso 3: Dividimos ambos lados por 2 para resolver: 2/2x > -6/2 = x>-3

EJERCICIO 4

Resuelve la desigualdad 3(x+2)>-9

Paso 1: Tenemos paréntesis, por lo que aplicamos la propiedad distributiva para eliminarlos: 3(x+2)>-9

3x+6>-9

Paso 2: Para despejar la variable, restamos 6 a ambos lados: 3x+6-6>-9-6 = 3x>-15

Paso 3: Para resolver, dividimos ambos lados por 3: 3/3x > -15/3 = x>-5

EJERCICIO 5

Resuelve la desigualdad 2(2x+4)+5>1

Paso 1: Simplificamos el paréntesis y combinamos términos semejantes

2(2x+4)+5>1 = 4x+8+5>1 = 4x+13>1

Paso 2: Despejamos la variable al restar 13 de ambos lados

4x+13-13>1-13 = 4x>-12

Paso 3: Tenemos que dividir por 4/4x > 12/4 = 4 x>-3

Ejercicios de sistemas de ecuaciones 2x2 resueltos

Resuelve el sistema de ecuaciones usando el método de sustitución:

Paso 1: No tenemos nada para simplificar.

Paso 2: Podemos resolver la primera ecuación para x x+2y=10 x=10-2y

Paso 3: Sustituimos la expresión x=10-2y en la segunda ecuación:

2x-y=5

2(10-2y)-y=5

20-4y-y=5

Paso 4: Resuelve para y:

20-4y-y=5

-5y=-15

y=3

Paso 5: Sustituimos y=3 en la primera ecuación: x+2y=10 x+2(3)=10 x=4