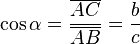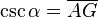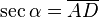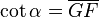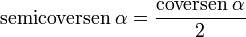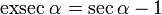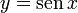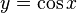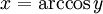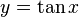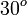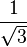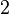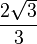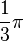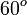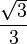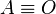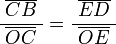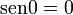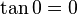Trigonometria examen

Enviado por Programa Chuletas y clasificado en Matemáticas

Escrito el 27 de Febrero de 2011 en español con un tamaño de 49,44 KB

Razones trigonométricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo $\alpha \,$ , correspondiente al vértice A, situado en el centro de la circunferencia.

El seno (abreviado como sen, o sin por llamarse "senos" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,

$\operatorname {sen} \, \alpha = \frac{\overline{CB}}{\overline{AB}} = \frac{a}{c}$

El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

$\cos\alpha = \frac{\overline{AC}}{\overline{AB}} = \frac{b}{c}$

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

$\tan\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{a}{b}$

Razones trigonométricas recíprocas

La Cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:

$\csc \alpha = \frac{1}{\operatorname {sen} \; \alpha} = \frac{c}{a}$

En el esquema su representación geométrica es:

$\csc \alpha = \overline{AG}$

La Secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:

$\sec \alpha = \frac{1}{\operatorname {cos} \; \alpha} = \frac{c}{b}$

En el esquema su representación geométrica es:

$\sec \alpha = \overline{AD}$

La Cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:

$\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}$

En el esquema su representación geométrica es:

$\cot \alpha = \overline{GF}$

Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés específico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse.

[editar]Otras funciones trigonométricas

Además de las funciones anteriores existen otras funciones trigonométricas, matemáticamente se pueden definir empleando las ya vistas, su uso no es muy corriente, pero si se emplean dado su sentido geométrico, veamos:

El seno cardinal o función sinc (x) definida:

$\operatorname {sinc} \; (x) = \frac{\sin(x)}{x}$

El verseno, es la distancia que hay entre la cuerda y el arco en una circunferencia, también se denomina sagita o flecha, se define:

$\operatorname {versen} \; \alpha = 1 - \cos \alpha$

El semiverseno, se utiliza en navegación al intervenir en el cálculo esférico:

$\operatorname {semiversen} \; \alpha = \frac {\operatorname {versen} \; \alpha }{2}$

El coverseno,

$\operatorname {coversen} \; \alpha = 1 - \operatorname {sen} \; \alpha$

El semicoverseno

$\operatorname {semicoversen} \; \alpha = \frac { \operatorname {coversen} \; \alpha }{2}$

El exsecante:

$\operatorname {exsec} \; \alpha = \sec \alpha - 1$

[editar]Funciones trigonométricas inversas

En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco,

$y= \operatorname {sen} \, x \,$

y es igual al seno de x, la función inversa:

$x = \operatorname {arcsen} \; y \,$

x es el arco cuyo seno vale y, o también x es el arcoseno de y.

si:

$y= \cos x \,$

y es igual al coseno de x, la función inversa:

$x = \arccos y \,$

x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.

si:

$y= \tan x \,$

y es igual al tangente de x, la función inversa:

$x = \arctan y \,$

x es el arco cuya tangente vale y, o x es igual al arcotangente de y.

Grados sexag.	seno	coseno	tangente	cosecante	secante	cotangente
$0 \;$	$0^o \,$	$\frac{\sqrt{0}}{2}=0$	$\frac{\sqrt{4}}{2}=1$	$0 \,$	$\nexists (\pm \infty) \,\!$	$1 \,$	$\nexists (\pm \infty) \,\!$
$\frac{1}{6}\pi$	$30^o \,$	$\frac{\sqrt{1}}{2}=\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$	$2 \,$	$\frac{2\sqrt{3}}{3}$	$\sqrt{3}$
$\frac{1}{4}\pi$	$45^o \,$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	$1 \,$	$\sqrt{2}$	$\sqrt{2}$	$1 \,$
$\frac{1}{3} \pi$	$60^o \,$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{1}}{2}=\frac{1}{2}$	$\sqrt{3}$	$\frac{2\sqrt{3}}{3}$	$2 \,$	$\frac{\sqrt{3}}{3}$
$\frac{1}{2} \pi$	$90^o \,$	$\frac{\sqrt{4}}{2}=1$	$\frac{\sqrt{0}}{2}=0$	$\nexists (\pm \infty) \,\!$	$1 \,$	$\nexists (\pm \infty) \,\!$	$0 \,$

Sentido de las funciones trigonométricas

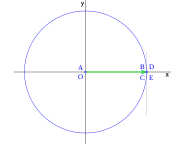
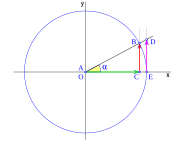
Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circunferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.

Nótese que el punto A es el vértice del triángulo, y O es el centro de coordenada del sistema de referencia:

$A \equiv O$

a todos los efectos.

La recta r, que pasa por O y forma un ángulo $\alpha \,$ sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.

Por semejanza de triángulos:

$\frac{\; \overline{CB} \;}{\overline{OC}} = \frac{\; \overline{ED} \;}{\overline{OE}}$

Los puntos E y B están en la circunferencia de centro O, por eso la distancia $\overline{OE}$ y $\overline{OB}$ son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:

$\operatorname {sen} \alpha = \overline{CB} \,$

$\cos \alpha = \overline{OC} \,$

$\tan \alpha = \overline{ED} \,$

tenemos:

$\frac{\operatorname {sen} \alpha}{ \cos \alpha} = \frac{\tan \alpha}{1}$

La tangente es la relación del seno entre el coseno, según la definición ya expuesta.

[editar]Primer cuadrante

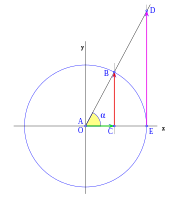
Para ver la evolución de las funciones trigonométricas según aumenta el ángulo, daremos una vuelta completa a la circunferencia, viéndolo por cuadrantes, los segmentos correspondientes a cada función trigonométrica variaran de longitud, siendo esta variación función del ángulo, partiendo en el primer cuadrante de un ángulo cero.

Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo $\alpha \,$ .

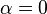Para $\alpha = 0 \,$ , tenemos que B, D, y C coinciden en E, por tanto:

$\operatorname {sen} 0 = 0 \,$

$\cos 0 = 1 \,$

$\tan 0 = 0 \,$

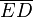Si aumentamos progresivamente el valor de $\alpha \,$ , las distancias $\overline{CB}$ y $\overline{ED}$ aumentarán progresivamente, mientras que $\overline{OC}$ disminuirá.

Percatarse que el punto B es de la circunferencia y cuando el ángulo aumenta se desplaza sobre ella.

El punto E es la intersección de la circunferencia con el eje x y no varia de posición.

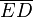Los segmentos: $\overline{OC}$ y $\overline{CB}$ están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero $\overline{ED}$ no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo $\alpha = 0,5 \pi \,$ rad, la recta r será la vertical que pasa por O. 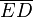Dos rectas verticales no se cortan, o lo que es lo mismo la distancia $\overline{ED}$ será infinita.

El punto C coincide con A y el coseno vale cero. El punto B esta en el eje y en el punto más alto de la circunferencia y el seno toma su mayor valor: uno.

Para un ángulo recto las funciones toman los valores:

$\operatorname {sen} \frac{\pi}{2} = 1 \,$

$\cos \frac{\pi}{2} = 0 \,$

$\tan \frac{\pi}{2} = \infty \,$

Entradas relacionadas:

Etiquetas: