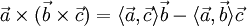Producto vectorial

Enviado por Javi y clasificado en Matemáticas

Escrito el 28 de Noviembre de 2007 en español con un tamaño de 6,97 KB

Definición

Sean dos vectores a y b en el espacio vectorial ?³. El producto vectorial entre a y b, como se mencionó antes, da como resultado un nuevo vector, al que llamaremos c. Para definir este nuevo vector es necesario especificar su módulo, dirección y sentido:

El módulo de c está dado por

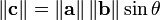
$\\\\\\\\left \\\\\\\\Vert \\\\\\\\mathbf{c} \\\\\\\\right \\\\\\\\Vert = \\\\\\\\left \\\\\\\\Vert \\\\\\\\mathbf{a} \\\\\\\\right \\\\\\\\Vert \\\\\\\\left \\\\\\\\Vert \\\\\\\\mathbf{b} \\\\\\\\right \\\\\\\\Vert \\\\\\\\sin{\\\\\\\\theta}$

donde ? es el ángulo entre a y b.

La dirección de c es tal que c es ortogonal a a y ortogonal a b.
El sentido en el que apunta el vector c está dado por la regla del sacacorchos.

El producto vectorial entre a y b se denota mediante a × b, por ello se lo llama también producto cruz. Para evitar confusiones con la letra x, algun

os autores denotan el producto vectorial mediante a ? b cuando escriben a mano.

El producto vectorial puede definirse de una manera más compacta de la siguiente manera:

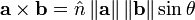
$\\\\\\\\mathbf{a} \\\\\\\\times \\\\\\\\mathbf{b} = \\\\\\\\hat n \\\\\\\\left \\\\\\\\Vert \\\\\\\\mathbf{a} \\\\\\\\right \\\\\\\\Vert \\\\\\\\left \\\\\\\\Vert \\\\\\\\mathbf{b} \\\\\\\\right \\\\\\\\Vert \\\\\\\\sin{\\\\\\\\theta}$

donde 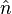$\\\\\\\\hat n$ es e

l versor ortogonal a los vectores a y b y su sentido está dado por la regla del sacacorchos y ? es, como antes, el ángulo entre a y b. A la regla del sacacorchos se la llama a menudo también regla de la mano derecha.

Relaciones entre los vectores definidos en esta sección.

Ejemplo

Sean los vectores:

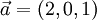
$\\\\\\\\vec a = (2,0,1)$

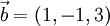
$\\\\\\\\vec b = (1,-1,3)$

El producto vectorial entre a y b se calcula como:

$\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b = \\\\\\\\begin{pmatrix} \\\\\\\\hat \\\\\\\\imath & \\\\\\\\hat \\\\\\\\jmath & \\\\\\\\hat k \\\\\\\\\\\\\\\\ 2 & 0 & 1 \\\\\\\\\\\\\\\\ 1 & -1 & 3 \\\\\\\\\\\\\\\\\\\\\\\\end{pmatrix}$

Expandiendo el determinante:

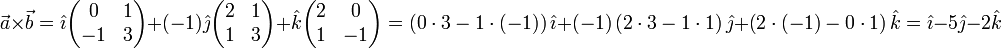
$\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b =\\\\\\\\hat \\\\\\\\imath \\\\\\\\begin{pmatrix} 0 & 1 \\\\\\\\\\\\\\\\ -1 & 3 \\\\\\\\\\\\\\\\\\\\\\\\end{pmatrix} +(-1) \\\\\\\\hat \\\\\\\\jmath \\\\\\\\begin{pmatrix} 2 & 1 \\\\\\\\\\\\\\\\ 1 & 3 \\\\\\\\\\\\\\\\\\\\\\\\end{pmatrix} +\\\\\\\\hat k \\\\\\\\begin{pmatrix} 2 & 0 \\\\\\\\\\\\\\\\ 1 & -1 \\\\\\\\\\\\\\\\\\\\\\\\end{pmatrix} =\\\\\\\\left ( 0 \\\\\\\\cdot 3 - 1 \\\\\\\\cdot (-1) \\\\\\\\right )\\\\\\\\hat \\\\\\\\imath +(-1) \\\\\\\\left ( 2 \\\\\\\\cdot 3 - 1 \\\\\\\\cdot 1 \\\\\\\\right )\\\\\\\\hat \\\\\\\\jmath +\\\\\\\\left ( 2 \\\\\\\\cdot (-1) - 0 \\\\\\\\cdot 1 \\\\\\\\right )\\\\\\\\hat k =\\\\\\\\hat \\\\\\\\imath - 5 \\\\\\\\hat \\\\\\\\jmath - 2 \\\\\\\\hat k$

Por lo tanto

$\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b = (1,-5,-2)$

Puede verificarse fácilmente que a × b es ortogonal al vector a y al vector b utilizando el producto escalar y verificando que éste da cero como resultado (condición de perpendicularidad de vectores).

Propiedades

Cualesquiera que sean los vectores 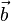$\\\\\\\\vec a$ , $\\\\\\\\vec b$ y $\\\\\\\\vec c$ en $\\\\\\\\mathbb{R}^3$ :

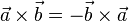$\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b = - \\\\\\\\vec b \\\\\\\\times \\\\\\\\vec a$ , (anticonmutatividad)
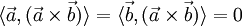$\\\\\\\\langle \\\\\\\\vec a , (\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b) \\\\\\\\rangle = \\\\\\\\langle \\\\\\\\vec b , (\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b) \\\\\\\\rangle = 0$ (el producto vectorial es perpendicular a cualquiera de los factores),
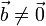Si $\\\\\\\\vec a \\\\\\\\neq \\\\\\\\vec 0$ y $\\\\\\\\vec b \\\\\\\\neq \\\\\\\\vec 0$ entonces 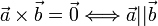$\\\\\\\\vec a \\\\\\\\times \\\\\\\\vec b = \\\\\\\\vec 0 \\\\\\\\Longleftrightarrow \\\\\\\\vec a || \\\\\\\\vec b$ (el producto cruz de dos vectores paralelos es cero).
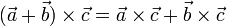$( \\\\\\\\vec a + \\\\\\\\vec b ) \\\\\\\\times \\\\\\\\vec c = \\\\\\\\vec a \\\\\\\\times \\\\\\\\vec c + \\\\\\\\vec b \\\\\\\\times \\\\\\\\vec c$ ,
$\\\\\\\\vec a \\\\\\\\times ( \\\\\\\\vec b \\\\\\\\times \\\\\\\\vec c ) = \\\\\\\\langle \\\\\\\\vec a , \\\\\\\\vec c \\\\\\\\rangle \\\\\\\\vec b - \\\\\\\\langle \\\\\\\\vec a , \\\\\\\\vec b \\\\\\\\rangle \\\\\\\\vec c$