Formulario Matemático: Trigonometría, Límites, Geometría y Más
Enviado por Programa Chuletas y clasificado en Matemáticas
Escrito el en 
español con un tamaño de 5,27 KB
| Ángulo (grados) | Ángulo (radianes) | Seno | Coseno | Tangente |
| 30 | π/6 | ½ | √3/2 | √3/3 |
| 45 | π/4 | √2/2 | √2/2 | 1 |
| 60 | π/3 | √3/2 | ½ | √3 |
| 90 | π/2 | 1 | 0 | ? |
| 120 | 2π/3 | √3/2 | -½ | -√3 |
| 135 | 3π/4 | √2/2 | -√2/2 | -1 |
| 150 | 5π/6 | ½ | -√3/2 | -√3/3 |
Recta tangente: y-y1= m(x-x1)
Asíntotas:
- A.V (Asíntota Vertical): Mirar el dominio.
- A.H (Asíntota Horizontal): Límites cuando tiendan a infinito y menos infinito; cuando hay A.H no hay A.O.
- A.O (Asíntota Oblicua): y=mx+n siendo la n= lim cuando x tiende a menos infinito de f(x)-mx y la m el límite cuando x tiende a menos infinito de f(x)/x, ésta no puede ser ni cero ni infinito.
L'Hôpital: Derivar arriba y derivar abajo. Cuando se da un cero por infinito, o sea A * B= B/1/A. En infinito menos infinito, o sea A-B si son raíces multiplicar y dividir por el conjugado y si es operar convertir en común denominador.
Límite de uno elevado a infinito es igual a e elevado al límite x el exponente por la base menos uno. La inversa de A es el adj de la traspuesta entre el determinante de A.
Ecuación de la esfera: (x-xo)2+(y-yo)2+(z-zo)2= R2; x2+y2+z2+ax+by+cz+d=0 siendo a, b y c el centro. Si la distancia es mayor que el radio es exterior, si son iguales es tangente y si es menor el plano corta a la esfera.
Puntos coplanarios: ab, ac, ad. Hacer determinante y si da cero, son coplanarios. Para hallar el área de un paralelogramo cogemos el vértice común y coger dos vectores que salgan de él. Hacer producto vectorial de ab y ad y hacer el módulo del resultado.
La intersección de dos planos se hace cogiendo una incógnita y poniéndole un parámetro.
Función objetivo (poner áreas) es aquella que me piden maximizar o minimizar f(x)= a2+b2+c2 (datos del problema). Se deriva la función y se iguala a cero. Te dará un valor de x.
Continuidad: f(x) en donde esté el igual; límite de f(x-) y lim de f(x+). Derivabilidad: límite de f'(x-) y límite de f(x+).
Teorema del valor medio: f(x) continua en [a,b] y derivable en (a,b) por lo que se cumple que existe un número desconocido que pertenece (a,b) tal que [f(b)-f(a)]/[b-a] sea igual a f'(c)
Teorema de Bolzano: f(x) continua en el intervalo [a,b] y signo de f(a) distinto al signo de f(b) y se cumple que existe un número desconocido que pertenece al intervalo (a,b) tal que f(c)=0.
Teorema de Rolle: f(x) es continua en [a,b] es derivable en (a,b) y f(a)=f(b) por lo que existe un número desconocido que pertenece a (a,b) tal que f'(c)=0
(A · B)-1 = B-1 · A-1
(k · A)-1 = k-1 · A-1
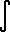xn dx = x(n+1) / (n+1) + C (n 
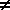-1) 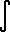1/x dx dx = ln|x| + C
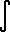sen x dx = -cos x + C
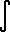cos x dx = sen x + C