Explorando las Matemáticas: Relaciones, Estadística y Logaritmos

Relaciones entre Coeficientes y Raíces

Para una función polinómica de tercer grado:

f(x) = ax³ + bx² + cx + d

Se cumplen las siguientes relaciones entre las raíces (X, B, γ) y los coeficientes:

• X + B + γ = -b/a
• XB + Xγ + Bγ = c/a
• XBγ = -d/a

Estadística

Ecuación de la recta:

y = ax + b

Donde:

• a = cov(x,y) / σx (pendiente)
• b = (media de y) - a * (media de x) (ordenada al origen)

Logaritmos

Definición: log_a(b) donde b > 0, a > 0 y a ≠ 1

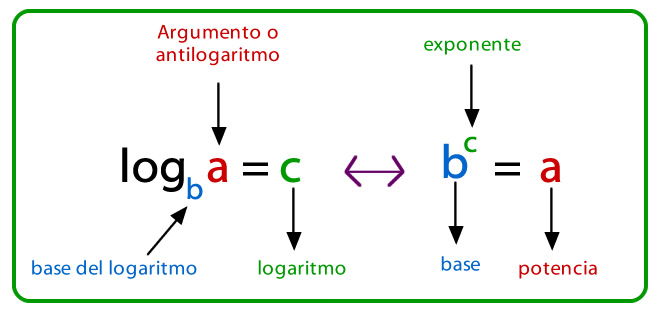
Propiedades:

1. log_a(1) = 0
2. log_a(b) + log_a(c) = log_a(b * c)
3. log_a(b) - log_a(c) = log_a(b / c)
4. n * log_a(b) = log_a(bⁿ)
5. log_a(b^1/n) = (1/n) * log_a(b) = log_a(ⁿ√b)
6. log_a(b) = log_c(b) / log_c(a) (cambio de base)

Teoría Estadística

Definiciones

Población: Conjunto de elementos sobre el cual se van a obtener datos para realizar el estudio estadístico. No toda la población se estudia, se toma una muestra. Ejemplo: Sucesión infinita de los resultados que se obtienen lanzando un dado.

Muestra: Subconjunto finito de elementos de una población. La representatividad de la muestra depende de su tamaño en relación a la población. Ejemplo: Resultados de 10 tiradas de dados.

Individuo: Es aquello sobre lo cual se toma medida. Ejemplo: empresas, exámenes.

Variables: Características que poseen los elementos de una población y que van a ser objeto de observaciones estadísticas. Es importante que se definan al comienzo del trabajo a realizar.

Valor: Cada uno de los posibles estados en los que puede presentarse una variable. Ejemplo: Si la variable es sexo, los valores de la variable son femenino y masculino.

Recorrido: Conjunto de valores posibles que puede tomar una variable.

Para elaborar tablas, cuadros y gráficos hay que tener en cuenta 3 aspectos:

1. Fuente u origen de los datos. Hay que distinguir si son datos de una población o una muestra.
2. Las características a las que se refieren los datos. Definición de variables.
3. La forma de medición usada en la recolección de los datos. Depende de la naturaleza de la variable. No es lo mismo medir una variable cuantitativa que cualitativa por ejemplo (esto se describe a continuación).

Clasificación de Variables

1. CUANTITATIVA: Aquellas en que se toma una unidad de medida. Con ellas se puede calcular media, mediana, modo, etc. Se utiliza escala numérica.
   1. CONTINUA: Los valores que puede tomar se consideran susceptibles de dividirse indefinidamente. Hay que tener en cuenta que la división indefinida es teórica, ya que el instrumento de medida es una limitante. Ejemplos: Salario, ingresos, tiempo.
   2. DISCRETA: No puede subdividirse indefinidamente. Ejemplos: Número de alumnos de una clase, número de integrantes de una familia.
2. CUALITATIVA: Son aquellas que están asociadas a características que no son cuantificables, a cada distinto tipo de resultado se le llama categoría. Se utiliza escala nominal.
   1. ORDINAL: Son aquellas que existe un orden natural, orden de preferencia. El recorrido se puede ordenar. Ejemplos: Talla de camisa XS – S – M – X – XL – XXL. Respuestas frente a una pregunta: No – Casi seguro que no – Casi seguro que sí – Sí.
   2. NOMINAL: El recorrido no puede ordenarse. Ejemplos: Estado civil, sexo, color de pelo.

Definiciones Teóricas de Estadística

1. Media: La media de una distribución es el valor central de la misma, alrededor del cual se distribuyen los valores. Siendo 𝑥₁, 𝑥₂, ⋯ , 𝑥_n los valores de la distribución: 𝑥̅ = (𝑥₁ + 𝑥₂ + ⋯ + 𝑥_n) / n = ∑_i=1ⁿ 𝑥_i / n
2. Varianza: La varianza indica cómo se dispersa cada valor respecto a su propia media. A mayor varianza, los datos están más dispersos.
3. Desviación Estándar: (Falta definición en el texto original)
4. Covarianza: La covarianza es una medida de resumen de dos variables cuantitativas. Permite decir de qué manera incide una variable en la otra. cov(x, y) = ∑ [(x_i - x̅)(y_i - y̅)] / n

Coeficiente de Correlación de Pearson

Si se trabajan con distintas unidades en x e y, la covarianza se ve afectada a pesar de corresponder al mismo gráfico, por tanto para solucionar el problema existe un indicador adimensionado que corresponde al coeficiente de correlación de Pearson. Determina cuando hay o no relación lineal entre dos variables y cuán fuerte es esa relación.

r_xy = cov(x, y) / (√var(x) * √var(y)) = cov(x, y) / (σ_x * σ_y)

Recta de Regresión

Dada una nube de puntos, en el caso que se pueda, podemos trazar una recta que se amolde a la nube, llamada recta de regresión para ver el grado de dependencia de ambas variables. Cuanto más se aproximen los puntos de la nube a la recta, mayor es la dependencia entre las dos variables.