Derivadas Formulas trigonometricas

Enviado por Programa Chuletas y clasificado en Matemáticas

Escrito el 4 de Junio de 2007 en español con un tamaño de 4,19 KB

Derivada de la función seno

A partir de la definición de la derivada de una función f(x):

$f'(x)=\\\\lim_{h\\\\to 0}{f(x+h)-f(x)\\\\over h}$

Por tanto si f(x) = sin(x)

$f'(x)=\\\\lim_{h\\\\to 0}{\\\\sin(x+h)-\\\\sin(x)\\\\over h}$

A partir de la identidad trigonométrica $sin(A + B) = sin(A)cos(B) + cos(A)sin(B)$ , se puede escribir

$f'(x)=\\\\lim_{h\\\\to 0}{\\\\sin(x)\\\\cos(h)+\\\\cos(x)\\\\sin(h)-\\\\sin(x)\\\\over h}$

Agrupando los términos cos(x) y sin(x), la derivada pasa a ser

$f'(x)=\\\\lim_{h\\\\to 0}{\\\\cos(x)\\\\sin(h)-\\\\sin(x)(1-\\\\cos(h))\\\\over h}$

Reordenando los términos y el límite se obtiene

$f'(x)=\\\\lim_{h\\\\to 0}{\\\\cos(x)\\\\sin(h)\\\\over h} - \\\\lim_{h\\\\to 0}{\\\\sin(x)(1-\\\\cos(h))\\\\over h}$

Ahora, como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener

$f'(x)=cos(x)\\\\lim_{h\\\\to 0}{\\\\sin(h)\\\\over h} - \\\\sin(x)\\\\lim_{h\\\\to 0}{(1-\\\\cos(h))\\\\over h}$

El valor de los límites

$\\\\lim_{h\\\\to 0}{\\\\sin(h)\\\\over h} \\\\quad\\\\text{y}\\\\quad \\\\lim_{h\\\\to 0}{(1-\\\\cos(h))\\\\over h}$

Son 1 y 0 respectivamente. Por tanto, si f(x) = sin(x),

$f'(x)=\\\\cos(x) \\\\,$

Si f(x) = cos(x)

$f'(x)=\\\\lim_{h\\\\to 0}{\\\\cos(x+h)-\\\\cos(x)\\\\over h}$

A partir de la identidad trigonométrica $cos(A + B) = cos(A)cos(B) ? sin(A)sin(B)$ , se puede escribir

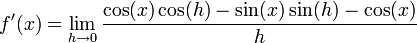
$f'(x)=\\\\lim_{h\\\\to 0}{\\\\cos(x)\\\\cos(h)-\\\\sin(x)\\\\sin(h)-\\\\cos(x)\\\\over h}$

Operando se obtiene

$f'(x)=\\\\lim_{h\\\\to 0}{\\\\cos(x)(\\\\cos(h)-1)-\\\\sin(x)\\\\sin(h))\\\\over h}$

Como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener

$f'(x)=cos(x)\\\\lim_{h\\\\to 0}{\\\\cos(h)-1\\\\over h} - \\\\sin(x)\\\\lim_{h\\\\to 0}{\\\\sin(h)\\\\over h}$

El valor de los límites

$\\\\lim_{h\\\\to 0}{\\\\sin(h)\\\\over h} \\\\quad\\\\text{y}\\\\quad \\\\lim_{h\\\\to 0}{(\\\\cos(h)-1)\\\\over h}$

Son 1 y 0 respectivamente. Por tanto, si f(x) = cos(x),

$f'(x)=-\\\\sin(x) \\\\,$

Etiquetas: