Representación Gráfica y Ecuaciones de Funciones Lineales y Cuadráticas
Enviado por Programa Chuletas y clasificado en Matemáticas
Escrito el en  español con un tamaño de 6,48 KB
español con un tamaño de 6,48 KB
Funciones Lineales: y = mx + n
Afines: y = mx + n
Constantes: y = n
Lineales: y = mx
Para representar la función en una gráfica a partir de la ecuación:
- Realizamos una tabla de valores.
- Con los puntos obtenidos, dibujamos la gráfica.
Para hallar la ecuación teniendo la gráfica:
- Buscamos dos puntos en la gráfica.
- Calculamos la pendiente (m): (y2 - y1) / (x2 - x1).
- Calculamos la ordenada al origen (n) escogiendo uno de los puntos y sustituyendo los valores de x, y, y m en la ecuación y = mx + n.
- Escribimos la ecuación completa.
Para hallar la ecuación con los puntos de corte:
- Primero, encontramos el punto de corte con el eje x (donde y = 0).
- Luego, encontramos el punto de corte con el eje y (donde x = 0).
Funciones Cuadráticas
Características
... Continuar leyendo "Representación Gráfica y Ecuaciones de Funciones Lineales y Cuadráticas" »
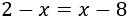
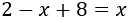
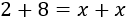
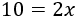
 vasco con un tamaño de 19,38 KB
vasco con un tamaño de 19,38 KB y
y  dos subconjuntos abiertos en
dos subconjuntos abiertos en  , donde
, donde  es simplemente conexo y el borde de
es simplemente conexo y el borde de  es una superficie regular o regular a trozos y cerrada.
es una superficie regular o regular a trozos y cerrada. , un campo vectorial de clase
, un campo vectorial de clase  , es decir,
, es decir,  cuenta con derivadas parciales de primer orden continuas.
cuenta con derivadas parciales de primer orden continuas.
 .
. es una
es una  es otra función continuamente diferenciable, pero de clase C1 en una región U, entonces:
es otra función continuamente diferenciable, pero de clase C1 en una región U, entonces:

 a:
a: