Ejercicios de fracciones
Enviado por Anónimo y clasificado en Matemáticas
Escrito el en  español con un tamaño de 8,02 KB
español con un tamaño de 8,02 KB
PROBLEMAS CON FRACCIONES (CONTINUACIÓN)
4.70 Una persona gastó ![]() del dinero que tenía.
del dinero que tenía.
Al día siguiente gastó ![]() del dinero que le quedó el día anterior.
del dinero que le quedó el día anterior.
Al siguiente día volvió a gastar ![]() del dinero que le quedó el último día y vio que en el bolsillo le quedaban 1000€.
del dinero que le quedó el último día y vio que en el bolsillo le quedaban 1000€.
¿Con cuánto dinero salió de casa?
Respuesta: Salió con 3375 €
Solución:
Vamos a resolverlo de un modo rápido por si has encontrado alguna duda.
Día 1º: Gasta ![]() del dinero que tenía al salir de casa.
del dinero que tenía al salir de casa.
Le quedan: 
Día 2º: Gasta ![]() del dinero que le quedó el día anterior:
del dinero que le quedó el día anterior:

Le quedan: 
Día 3º: Gasta ![]() del dinero que le quedó el día anterior:
del dinero que le quedó el día anterior:

Le quedan: 
Nos dice el problema que al tercer día le quedaron 1000€. Esto quiere decir que ![]() es lo mismo que 1000€ y el dinero... Continuar leyendo "Ejercicios de fracciones" »
es lo mismo que 1000€ y el dinero... Continuar leyendo "Ejercicios de fracciones" »

 es el conjunto de existencia de la misma, es decir, los valores para
los cuales la función está definida. Es el conjunto de todos los
objetos que puede transformar, se denota
es el conjunto de existencia de la misma, es decir, los valores para
los cuales la función está definida. Es el conjunto de todos los
objetos que puede transformar, se denota  o bien
o bien 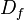 .
. El dominio de esta función es
El dominio de esta función es 
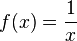 El dominio de esta función es
El dominio de esta función es  puesto que la función no está definida para x = 0 (la división por cero no existe!).
puesto que la función no está definida para x = 0 (la división por cero no existe!). El dominio de esta función es
El dominio de esta función es  ya que los logaritmos están definidos sólo para números positivos.
ya que los logaritmos están definidos sólo para números positivos. El dominio de esta función es
El dominio de esta función es 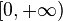 porque la raíz de un número negativo no existe en el campo de los Reales.
porque la raíz de un número negativo no existe en el campo de los Reales.