Que es un polinomio constante
Enviado por Chuletator online y clasificado en Matemáticas
Escrito el en  español con un tamaño de 8,44 KB
español con un tamaño de 8,44 KB
COMPONENTES DE UN POLINOMIO
-Término-Coeficiente-Grado del polinomio-Coeficiente indeterminado
OPERACIONES CON POLINOMIO
-Suma y Resta:
se suman o restan los términos de igual exponente.-Multiplicación:
se aplica usando la propiedad distributiva.-División:
1)Ordenar el polinomio de forma decreciente.
2) Primero tomar en cuenta el signo, luego el número y por último la variable. OJO-El dividendo debe ser igual o mayor que el divisor (el grado).
Procedimiento:
1) Ordene de forma decreciente
2) Forme una cuadrilla donde solo se colocan los coeficientes incluyendo los ceros y el coeficiente indeterminado.
3) Seleccione la raíz del polinomio que tiene que ser divisor el coeficiente indeterminado.
4) Cada vez que halle una raíz le baja el orden

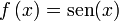

















 gallego con un tamaño de 1,04 KB
gallego con un tamaño de 1,04 KB