Desarrollo en Serie de Fourier (DSF)

Enviado por Anónimo y clasificado en Otras materias

Escrito el 28 de Enero de 2008 en español con un tamaño de 6,48 KB

El análisis de Fourier es una herramienta matemática utilizada para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinitesimal de funciones senoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicando sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces Análisis armónico.

Es una aplicación usada en muchas ramas de la ingeniería, además de ser una herramienta sumamente útil en la teoría matemática abstracta. Areas de aplicación incluyen análisis vibratorio , acustica, óptica, procesamiento de imágenes y señales,y compresión de datos. En ingeniería, para el caso de los sistemas de telecomunicaciones, y a través del uso de los componentes espectrales de frecuencia de una señal dada, se puede optimizar el diseño de un sistema para la señal portadora del mismo. Refierase al uso de un analizador de espectros.

Las series de Fourier poseen la forma:

$y(x) = \\\\\\\\\\\\\\\\frac{a_0}{2} + \\\\\\\\\\\\\\\\sum_{n=1}^\\\\\\\\\\\\\\\\infty\\\\\\\\\\\\\\\\left[a_n\\\\\\\\\\\\\\\\cos(nx)+b_n\\\\\\\\\\\\\\\\operatorname{sen}(nx)\\\\\\\\\\\\\\\\right]$

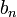donde $a_n \\\\\\\\\\\\\\\\,\\\\\\\\\\\\\\\\!$ y $b_n \\\\\\\\\\\\\\\\,\\\\\\\\\\\\\\\\!$ se denominan coeficientes de Fourier de la serie de Fourier de la función

Definición

Si $f$ es una función (o señal) periódica y su período es $T$ , la serie de Fourier asociada a $f$ es:

$f(t) \\\\\\\\\\\\\\\\sim \\\\\\\\\\\\\\\\frac{a_0}{2} + \\\\\\\\\\\\\\\\sum_{n=1}^\\\\\\\\\\\\\\\\infty\\\\\\\\\\\\\\\\left[a_n\\\\\\\\\\\\\\\\cos\\\\\\\\\\\\\\\\frac{n\\\\\\\\\\\\\\\\pi}{T}t+b_n\\\\\\\\\\\\\\\\operatorname{sen}\\\\\\\\\\\\\\\\frac{n\\\\\\\\\\\\\\\\pi}{T}t\\\\\\\\\\\\\\\\right].$

$a n$ y $b n$ son los coeficientes de Fourier que toman los valores:

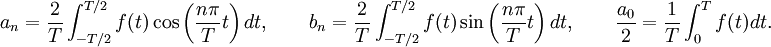
$a_n = \\\\\\\\\\\\\\\\frac{2}{T} \\\\\\\\\\\\\\\\int_{-T/2}^{T/2} f(t) \\\\\\\\\\\\\\\\cos \\\\\\\\\\\\\\\\left( \\\\\\\\\\\\\\\\frac{n \\\\\\\\\\\\\\\\pi}{T} t \\\\\\\\\\\\\\\\right) dt, \\\\\\\\\\\\\\\\qquad b_n=\\\\\\\\\\\\\\\\frac{2}{T} \\\\\\\\\\\\\\\\int_{-T/2}^{T/2} f(t) \\\\\\\\\\\\\\\\sin \\\\\\\\\\\\\\\\left(\\\\\\\\\\\\\\\\frac{n\\\\\\\\\\\\\\\\pi}{T}t\\\\\\\\\\\\\\\\right) dt, \\\\\\\\\\\\\\\\qquad \\\\\\\\\\\\\\\\frac{a_0}{2} = \\\\\\\\\\\\\\\\frac{1}{T} \\\\\\\\\\\\\\\\int_{0}^{T} f(t)dt .$

Por la identidad de Euler, las fórmulas de arriba pueden expresarse también en su forma compleja:

$f(t) \\\\\\\\\\\\\\\\sim \\\\\\\\\\\\\\\\sum_{n=-\\\\\\\\\\\\\\\\infty}^{\\\\\\\\\\\\\\\\infty} c_{n}\\\\\\\\\\\\\\\\,e^{2\\\\\\\\\\\\\\\\pi i\\\\\\\\\\\\\\\\frac{n}{T}t}.$

Los coeficientes ahora serían

$c_n=\\\\\\\\\\\\\\\\frac{1}{T}\\\\\\\\\\\\\\\\int_{-T/2}^{T/2} f(t)\\\\\\\\\\\\\\\\,e^{-2\\\\\\\\\\\\\\\\pi i\\\\\\\\\\\\\\\\frac {n}{T}t}\\\\\\\\\\\\\\\\,dt.$

Lo más frecuente es trabajar con funciones de período $2?$ .

== Teorema de máximos y mínimos locales y un número finito de discontinuidades, de período 2p. Sean

$a_n = \\\\\\\\\\\\\\\\frac{1}{p} \\\\\\\\\\\\\\\\int_{-p}^{p}f(x) \\\\\\\\\\\\\\\\operatorname{cos} \\\\\\\\\\\\\\\\frac{n \\\\\\\\\\\\\\\\pi x} {p} dx,$

$b_n = \\\\\\\\\\\\\\\\frac{1}{p} \\\\\\\\\\\\\\\\int_{-p}^{p}f(x) \\\\\\\\\\\\\\\\operatorname{sen} \\\\\\\\\\\\\\\\frac{n \\\\\\\\\\\\\\\\pi x} {p} dx,$

entonces la serie converge a f(x).

Ingeniería

El análisis de señales en el dominio del tiempo se realiza a través de las series de Fourier, por cuanto es muy común, reemplazar la variable x por ?t, resultando las componentes:

$C_n = \\\\\\\\\\\\\\\\frac{1}{T}\\\\\\\\\\\\\\\\int_{t_1}^{t_2} f(t) e^{-j \\\\\\\\\\\\\\\\omega_n t}\\\\\\\\\\\\\\\\, dt,$

Por lo tanto:

$f(t) = \\\\\\\\\\\\\\\\sum_{n=-\\\\\\\\\\\\\\\\infty}^{+\\\\\\\\\\\\\\\\infty} C_n e^{j \\\\\\\\\\\\\\\\omega_n t}$

Aplicaciones

Generación de formas de onda de corriente o tensión eléctrica por medio de la superposición de senoides generados por osciladores eléctrónicos de amplitud variable cuyas frecuencias ya están determinadas.
Análisis en el comportamiento armónico de una señal
Reforzamiento de señales.
Estudio de la respuesta en el tiempo de una variable circuital eléctrica donde la señal de entrada no es senoidal o cosenoidal, mediante el uso de transformadas de Laplace y/o Solución en regimen permanente senoidal en el dominio de la frecuencia.

Entradas relacionadas:

Etiquetas: